[논문 같이 읽기] Denoising Diffusion Probabilistic Models

논문 링크 :

Denoising Diffusion Probabilistic Models

유투브 설명 링크 : 

수식 설명 링크 : 

[논문공부] Denoising Diffusion Probabilistic Models (DDPM) 설명

Diffusion model 유투브 자료 (DDPM, DDIM, Score-based, SDE, ODE 등등) :

 

최근 스터디를 진행하고 있는 diffusion model의 논문입니다.

수식에 대한 부분은 수식이 나올 때

링크 자료를 참고하여 최대한 줄글로 풀어보겠습니다.

수식을 최대한 줄글로 풀어쓰려고 하였는데 오류가 있다면 지적해 주시기 바랍니다.

 

우리는 비평형 열역학 고려 사항에서 영감을 받은 잠재 변수 모델 클래스인 확산 확률 모델을 사용하여 높은 품질의 이미지 합성 결과를 제시합니다.

최고의 결과는 diffusion 확률 모델과 Langevin 역학과 맞먹는 잡음 제거 점수와의 새로운 연결에 따라 설계된

가중된 변분 한계를 학습하여 얻어졌습니다.

그리고 우리의 모델은 자동회귀적 디코딩의 일반화로 해석될 수 있는

점진적인 손실 분해 방식을 자연스럽게 받아들였습니다.

(* Autoregressive decoding : 이전 time step의 정보를 사용해 현재 time step의 값을 생성하는 방식으로 decoding(복호화)을 수행)

조건이 없는 CIFAR10 데이터 세트에서, 우리는 9.4의 Inceptioin score 와 3.17의 SOTA FID score를 얻었습니다.

(* Inception score : Sharpness와 Diversity의 곱으로 표현되는 점수, 생성 이미지의 예측 수월성 X 생성 이미지의 다양성, 점수가 클 수록 좋은 모델)

(* FID score : 시험 이미지의 feature와 생성 이미지의 feature를 비교하여 얻어지는 점수, 평균과 공분산의 계산으로 표현, 점수가 작을 수록 test image 와 generated image의 차이가 적다는 의미이기 때문에 좋은 모델)

(4) 생성 모델의 평가

 

GANs의 그것과 비슷한 이미지를 생성하는 에너지-기반의 모델링 및 스코어 매칭에는 현저한 발전이 있었습니다.

(* energy-based modeling : 특정 상태의 확률을 나타내는 energy function을 사용하는 모델)

(* score matching : 점수 매칭, 실험군과 대조군의 score를 매칭, 비교)

Energy-Based Models · 딥러닝

 

diffusion 확률 모델(간결성을 위해 "diffusion model"이라 부를 것)은 유한 시간 이후에 데이터와 맞먹는 샘플을 생성하는 변분 추론을 사용하여 학습되는 매개변수화 된 Markov chain입니다.

이 chain의 전이는 diffusion 절차를 역전시키기 위해 학습되며 이것은 신호가 파괴될 때까지 샘플링의 반대 방향으로 데이터에 점진적으로 잡음을 추가하는 Markov chain입니다.

샘플링 chain 전이는 조건부 Gaussian로 설정하기에 충분하고 이것은 특히 단순 신경망 매개변수화에 허용됩니다.

변분추론(Variational Inference) · ratsgo's blog

마르코프 체인에 관하여 - PuzzleData

 

diffusion 모델은 정의하기에 간단하고 학습하기에 효율적입니다. 하지만 우리가 아는 한, 그것이 고품질의 샘플을 생성할 수 있는지에 대해서는 입증된 바가 없습니다.

우리는 diffusion 모델이 실제로 고품질의 샘플을 생성할 수 있다는 것을 보여주고 가끔씩은 다른 유형의 생성 모델의 발표된 결과들보다 더 낫다는 것을 보여줄  것입니다.

추가적으로, 우리는 diffusion 모델의 특정한 매개 변수화가 학습 중 다중 잡음 수준에 대한 잡음 제거 점수 매칭과 샘플링 중 변화된 Langevin 역학과 동등하다는 것을 밝혀낸다는 것을 보여줄 것입니다.

(certain diffusion model parameterization == denoising score matching over multiple noise levels(training), annealed Langevin dynamics (sampling))

우리는 최고의 샘플 품질 결과를 이 매개변수화를 사용해 얻었으며, 따라서 우리는 이 동등함이 우리의 주요 공헌 중 하나라고 여기고 있습니다.

(* 매개변수화, parameterization : 내포적 방정식으로 정의된 곡선, 표면, 또는 더 일반적으로, 다수 또는 다양성의 매개 변수 방정식을 찾는 과정, parameterization은 매개변수로 표현한다는 것을 의미합니다.)

Parametrization (geometry) - Wikipedia

 

그 샘플 품질에도 불구하고, 우리의 모델은 다른 likehood-기반 모델에 비할 정도의 log likelihoods를 가지지 못합니다. (우리의 모델은 하지만 변화된 중요도 샘플링이 에너지 기반 모델과 스코어 매칭에 대해 생성하는 것으로 알려진 많은 추정치 보다는 더 나은 log likelikhoods를 가집니다.)

우리 모델의 손실이 없는 codelength의 대부분이 감지할 수 없는 이미지 세부 사항을 묘사하는 데 사용된다는 것을 발견했습니다.

우리는 손실 압축의 언어로 이 현상에 대한 보다 세련된 분석을 제시하고 diffusion 모델의 샘플링 절차가 자동회귀 모델에서 일반적으로 가능한 것을 광범위하게 일반화하는 비트 순서에 따른 자동회귀 디코딩과 유사한 점진적 디코딩의 일종임을 보여줍니다.

 

Diffusion model은 $p_{\theta}(X_{0})  :=  \int p_{\theta}(X_{0:T})dX_{1:t}$ 식의 잠재 변수 모델입니다.

여기서 $X_{1}$,...,$X_{T}$는 data $X_{0}  \sim q(X_{0})$ (* q(X0)에 비례하는 데이터 X0)의 차원과 같은 차원의 잠재 변수입니다.

결합 분포 $p_{\theta}(X_{0:T})$는 반대 과정으로 불립니다. 그리고 그것은 $p(X_{T})=\mathcal{N}(X_{T} ;0,I)$ 에서 시작하는 학습된 Gaussian 전이를 갖는 Markov chain으로 정의됩니다.

(* $:=$ , definition, 정의)

(* $a:b$ , from a to b, a와 b 사이의 모든 step 값, 방향성은 없음, 축약 표현)

(* $\int$ , 적분 표현 / * $dX$, X에 대한 극소 변화 표현)

(* $\sim$ , 비례 표현)

$X_{0}$의 분포 $p_{\theta}$는 $X$가 $X_{1}$부터 $X_{T}$까지 극소 변화할 때, $X_{0}$부터 $X_{T}$까지의 결합 분포 $p_{\theta}$를 적분한 것으로 정의됩니다.

$p(X_{T})$는 평균 $0$, 분산 $I$(항등 행렬)을 따르는 $X_{T}$의 정규 분포와 같습니다.

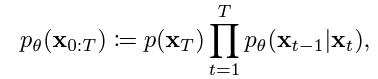
$X_{0}$부터 $X_{T}$까지의 결합 분포 $p_{\theta}$는 $X_{t}$를 조건으로 하는 $X_{t-1}$의 분포 $p_{\theta}$의 $t=1$부터 $T$까지의 부분곱에 $p(X_{T})$를 곱한 것으로 정의됩니다.

(위의 식 Latex 연습, $p_{\theta}(X_{0:T})  := p(X_{T}) \prod_{t=1}^{T}p_{\theta}(X_{t-1}|X_{t})$)

$X_{t}$를 조건으로 하는 $X_{t-1}$의 분포 $p_{\theta}$는 평균 $\mu_{\theta}(x_{t},t)$, 분산 $\Sigma_{\theta}(x_{t},t)$를 따르는 $X_{t-1}$의 정규 분포로 정의됩니다.

 

Diffusion model을 다른 유형의 잠재 변수 모델과 구별짓는 것은 forward process(순방향 과정) 또는 diffusion process라고 불리는 근사 사후 $q(X_{1:T}|X_{0})$가 분산 스케줄 $beta_{1}$,...,$beta_{T}$에 따라 데이터에 Gaussian 잡음을 점진적으로 추가하는 Markov chain에 고정된다는 것입니다.

$X_{0}$를 조건으로 하는 $X_{1}$부터 $X_{T}$까지의 결합 분포 $q$는 $X_{t-1}$을 조건으로 하는 $X_{t}$의 분포 $q$를 $t=1$부터 $T$까지 연속적으로 곱한 것으로 정의됩니다.

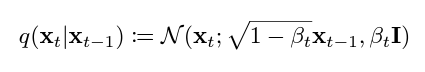
$X_{t-1}$을 조건으로 하는 $X_{t}$의 분포 $q$는 평균 $\sqrt(1-\beta_{t})X_{t-1}$, 분산 $\beta_{t}I$를 따르는 $X_{t}$의 정규 분포로 정의됩니다.

 

학습은 negative log likelihood에 근거한 보통의 변분 경계를 최적화하는 것으로 수행됩니다.

$X_{0}$의 분포 $p_{\theta}$의 negative log 값의 기대값은

$p(X_{T})$의 negative log 값과 t가 1보다 클 때의 결합 분포 $p_{\theta}(X_{t-1}|X_{t})$를 결합 분포 $q(X_{t}|X_{t-1})$로 나눈 것의 합계의 negative log 값을 더한 것의 $q$에 대한 기대값과 같은

결합 분포 $p_{\theta}(X_{0:T})$를 결합 분포 $q(X_{1:T}|X_{0})$로 나눈 것의 negative log 값의 $q$에 대한 기대값 보다 작으며

이것은 $L$(lower bound, 하한)로 정의됩니다.

(*$\mathbb{E}$: expected value operator, 기대값 연산자)

Understanding the Variational Lower Bound

 

순방향 과정의 분산 $\beta_{t}$는 재매개변수화로 학습되거나 하이퍼 파라미터로 일정하게 유지될 수 있으며, 역방향  과정의 표현력은 $p_{\theta}(X_{t-1}|X_{t})$에서 Gaussian 조건의 선택에 의해 부분적으로 보장됩니다.

왜냐하면 양 과정이 $\beta_{t}$가 작을 때 동일한 함수식을 가지기 때문입니다.

순방향 과정의 주목할 만한 특성은 임의의 시간 단계 $t$에서 $1-\beta_{t}$로 정의되는 $\alpha_{t}$와 $\alpha_{s}$의 $s=1$부터 $t$까지의 부분곱으로 정의되는 $\bar{\alpha}$ 기호를 사용하는 닫힌 형식으로 그것이 $Xt$에 대한 샘플링을 허용한다는 것입니다.

우리는 (4)번 수식을 가지게 됩니다.

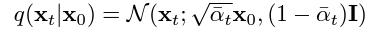
$X_{0}$를 조건으로 하는 $X_{t}$의 분포 $q$는 평균 $\sqrt(\bar{\alpha_{t}})X_{0}$, 분산 $(1-\bar{\alpha_{t}})I$를 따르는 $X_{t}$의 정규 분포와 같습니다.

 

효율적인 학습은 확률적 경사 하강과 함께 $L$의 임의 항을 최적화함으로써 가능해집니다. 추가적인 개선은 $L$을 (5)와 같이 재작성하는 분산 감소에서 나옵니다.

$L_{T}$로 일컬어지는 $q(X_{T}|X_{0})$와 $p(X_{T})$의 KL divergence와

$L_{t-1}$로 일컬어지는 t가 1보다 클 때의 $q(X_{t-1}|X_{t},X_{0})$와 $p(X_{t-1}|X_{t})$의 KL divergence의 합계에

$L_{0}$로 일컬어지는 $p_{\theta}(X_{0}|X_{1})의 negative log 값을 더한 값의 q에 대한 기대값으로 표현됨

초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기

자연어처리를 위한 Negative Log Likelihood

 

방정식 (5)는 KL divergence를 사용하여 $p_{\theta}(X_{t-1}|X_{t})$를 순방향 과정 사후들과 직접적으로 비교합니다. 이것은 $X_{0}$를 조건으로 할 때 추적 가능합니다.

결과적으로, 방정식 (5)의 모든 KL divergences들은 Gaussian 사이의 비교들이고, 따라서 그들은 고분산의 MonteCarlos 추정치 대신 닫힌 형식의 표현을 사용하여 Rao-Blackwellized 방식으로 계산될 수 있습니다.

$X_{t}$와 $X_{0}$를 조건으로 하는 $X_{t-1}$의 분포 $q$는 평균 $\tilde{\mu}_{t}(X_{t},X_{0})$, 분산 $\tilde{\beta}_{t}I$를 따르는 $X_{t-1}$의 정규 분포와 같습니다.

$\tilde{\mu}_{t}(X_{t},X_{0})$와 $\tilde{\beta}_{t}$의 정의. 각각 $X_{0}$와 $X_{t}$, $\beta_{t}$로 표현.

Tilde - Wikipedia

Closed Form – Wanho Choi

 

 

Diffusion model은 잠재 변수 모델의 제한된 클래스로 보여질 수도 있지만, 그것은 구현에 많은 자유도를 허락합니다. 순방향 과정에서의 분산 $\beta_{t}$와 역방향 과정에서의 모델 아키텍쳐 및 Gaussian 분포의 매개변수화를 선택해야 합니다.

우리는 diffusion model과 denoising score matching의 새로운 명시적 연결을 설정하여 그것이 diffusion model을 위한 단순화되고, 가중된 변분 경계 목표로 이어지게 하였습니다.

궁극적으로 우리의 모델 설계는 단순성과 경험적 결과들에 의해 정당화되었습니다.

 

우리는 순방향 과정 분산 $\beta_{t}$가 재매개변수화를 통해 학습 가능하다는 사실을 무시하였고 대신에 그것을 상수로 고정시켰습니다.

그리하여, 우리의 구현에서, 근사 사후 $q$는 학습 가능한 파라미터를 가지지 않습니다.

그러므로 $L_{T}$는 학습 동안 변함없으며 무시될 수 있습니다.

 

이제 우리는 $t$가 1에서 $T$사이의 값일 때, $p_{\theta}(X_{t-1}|X_{t}) = \mathcal{N}(X_{t-1};\mu_{\theta}(X_{t},t),\sum_{\theta}(X_{t},t))$에서의 우리의 선택에 대해 논하고자 합니다.

먼저, 우리는 $\sum_{\theta}(X_{t},t) = \sigma^2_{t}I$를 훈련되지 않은 시간 종속 상수로 설정하였습니다.

실험적으로 $\sigma^2_{t}=\beta_{t}$와

$\sigma^2_{t}=\tilde{\beta}_{t}=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_{t}}\beta_{t}$는 모두 유사한 결과를 가졌습니다.

첫 번째 선택은 $X_{0} \sim \mathcal{N}(O,I)$에 대해 최적이고,

두 번째는 $X_{0}$가 결정적으로 한 점에 설정되는 경우에 최적입니다.

이들은 좌표 방식 단위 분산 데이터에 대한 역방향 과정 엔트로피의 상한 및 하한에 해당하는 두 극단적인 선택들입니다.

 

두 번째로, 우리는 평균 $\mu_{\theta}(X_{t},t)$를 표현하였습니다.

우리는 $L_{t}$에 대한 후속 분석으로부터 동기 부여된 특정한 매개변수화를 제안합니다.

$p_{\theta}(X_{t-1}|X_{t}) = \mathcal{N}(X_{t-1};\mu_{\theta}(X_{t},t), \sigma^2_{\theta}I)$로 다음과 같이 쓸 수 있습니다.

$L_{t-1}$은 $\tilde{\mu}_{t}(X_{t}, X_{0})$에서 $\mu_{\theta}(X_{t},t)$를 뺀 값의 norm의 제곱에 $\frac{1}{2\sigma^2_{t}}$를 곱한 것의 q에 대한 기대값에 상수 C를 더한 값과 같습니다.

l1-norm과 l2-norm에 대하여

What is the meaning of super script 2 subscript 2 within the context of norms?

 

여기에서 상수 C는 $\theta$에 종속되지 않는 상수입니다.

그러므로, 우리는 $\mu_{\theta}$의 가장 직접적인 매개변수화가 순방향 과정 사후 평균, $\bar{\mu}_{t}$를 예측하는 모델임을 알 수 있습니다.

그러나 우리는 방정식 (8)을 방정식 (4)를 $X_{t}(X_{0},\epsilon) = \sqrt{\bar{\alpha}_{t}}X_{0} + \sqrt{1-\bar{\alpha}_{t}}\epsilon$, $\epsilon \sim \mathcal{N}(0,I)$로 재매개변수화하고

순방향 과정 사후 공식을 적용함으로써 더욱 확장시킬 수 있습니다.

$X_{t}(X_{0}, \epsilon)$은 $\epsilon$이 $\mathcal{N}(0,1)$을 따를 때, $\sqrt{\bar{\alpha}_{t}}X_{0}$과 $\sqrt{1-\bar{\alpha}_{t}}\epsilon$의 합과 같습니다.

$L_{t-1}-C$는 $\tilde{\mu}_{t}(X_{t}(X_{0}, \epsilon), \frac{1}{\sqrt{\bar{\alpha}_{t}}}(X_{t}(X_{0}, \epsilon) - \sqrt{1-\bar{\alpha}_{t}}\epsilon))$에서 $\mu_{\theta}(X_{t}(X_{0}, \epsilon), t)$를 뺀 값의 norm의 제곱에 $\frac{1}{2\sigma^2_{t}}$를 곱한 값의 $X_{0}, \epsilon$에 대한 기대값이고

이는 다시  $\frac{1}{\sqrt{\alpha}_{t}}(X_{t}(X_{0}, \epsilon) - \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon)$에서 $\mu_{\theta}(X_{t}(X_{0}, \epsilon), t)$를 뺀 값의 norm의 제곱에 $\frac{1}{2\sigma^2_{t}}$를 곱한 값의 $X_{0}, \epsilon$에 대한 기대값으로 표현됩니다.

 

방정식 (10)은 $\mu_{\theta}$가 주어진 $X_{t}$에서 $\frac{1}{\sqrt{\alpha}_{t}}(X_{t} - \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon)$를 예측해야 함을 나타냅니다. 

$X_{t}$가 모델에 대한 입력으로 사용될 수 있으므로, 우리는 매개변수화를 선택할 수 있습니다. 

$\mu_{\theta}(X_{t},t)$를 $\tilde{\mu}_{t}$의 식으로 풀고 이를 다시 풀어 $X_{t}와 \epsilon_{\theta}(X_{t},{t})$의 식으로 표현.

 

여기에서 $\epsilon_{\theta}$는 $X_{t}$에서 $\epsilon$을 예측하기 위한 함수 근사치입니다.

$p_{\theta}(X_{t-1}|X_{t})$를 따르는 $X_{t-1}$을 샘플링하는 것은 $z$가 $\mathcal{N}(0,I)$를 따를 때, $X_{t-1} = \frac{1}{\sqrt{\alpha}_{t}}(X_{t} - \frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}}\epsilon_{\theta}(X_{t},t)) + \sigma_{t}z$를 계산하는 것과 같습니다.

전체 샘플링 절차인 알고리즘 2는 데이터 밀도의 학습된 기울기로 $\epsilon_{\theta}$를 갖는 Langevin dynamics와 유사합니다.

더욱이, 방정식 (11)의 매개변수화를 사용하면 방정식 (10)은 다음과 같이 단순화됩니다.

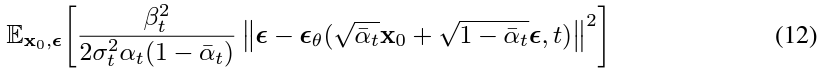
$\mu_{\theta}(X_{t}(X_{0}, \epsilon), t)$를 풀고 전개하여 $\epsilon$과 $\epsilon_{\theta}$에 대한 식으로 표현

 

이것은 $t$로 인덱싱된 여러 잡음 척도에 대한 denoising score matching과 유사합니다.

방정식 (12)가 Langevin-like 역방향 과정 (11)에 대한 변분 경계(의 한 항과)와 같기 때문에,

우리는 denoising score matching과 유사한 목표를 최적화하는 것이

Langevin dynamics를 닮은 샘플링 체인의 유한-시간 한계를 맞추기 위해 변분 추론을 사용하는 것과 동등하다는 것을 알 수 있습니다.

요약하자면, 우리는 역방향 과정 평균 함수 근사치 $\mu_{\theta}$를 학습시켜 $\tilde{\mu}_{t}$를 예측하거나, 그것의 매개변수화를 수정하고 학습시켜 $\epsilon$을 예측하게 할 수 있습니다.

($X_{0}$를 예측하는 가능성도 역시 존재하지만 우리는 실험 초기에 이것이 샘플 품질을 악화시킨다는 것을 발견하였습니다.)

우리는 $\epsilon$-예측 매개변수화 둘 다 Langevin dynamics와 유사하고 denoising score matching과 유사한 목표에 대한 diffusion model의 변분 경계를 단순화시킨다는 것을 보여주었습니다.

그럼에도 불구하고, 이것은 단지 $p_{\theta}(X_{t-1}|X_{t})$의 다른 매개변수화이기 때문에 우리는 Section 4에서 $\epsilon$을 예측하는 것과 $\tilde{\mu}_{t}$를 예측하는 것을 비교하는 ablation으로 그것의 효과를 입증할 것입니다.

 

우리는 {0, 1, ..., 255}의 정수로 구성된 이미지 데이터가 [-1,1]로 선형적으로 스케일되었다고 가정하였습니다.

이것은 신경망 역방향 과정이 표준 정규 사전 $p(X_{T})$에서 시작하는 일관되게 스케일된 입력에서 작동하도록 보장합니다.

이산 log likelihoods를 얻기 위해, 우리는 역방향 과정의 마지막 항을 Gaussian $\mathcal{N}(X_{0};\mu_{\theta}(X_{1},1)), \sigma^2_{1}I))$에서 파생된 독립적인 이산 디코더로 설정하였습니다.

$X_{1}$을 조건으로 하는 $X_{0}$의 분포 $p_{\theta}$는 $x$가 극소 변화할 때, 평균 $\mu^{i}_{\theta}(X_{1},1)$ 분산 $\sigma^2_{1}$을 따르는 $x$의 정규 분포의 $\delta-(x^{i}_{0})$부터 $\delta+(x^{i}_{0})$까지의 적분값의 $i=1$ 부터 $D$까지의 부분곱과 같습니다.

 

여기에서 $D$는 데이터 차원이고 $i$ 위첨자는 한 좌표의 추출을 나타냅니다.

(조건부 자동 회귀 모델과 같은 더 강력한 디코더를 대신 통합하는 것이 더 직접적일 테지만, 향후 작업으로 남기겠습니다.)

VAE 디코더와 자동 회귀 모델에서 사용된 분할된 연속 분포와 유사하게, 우리의 선택은 변분 경계가 데이터에 잡음을 추가하거나 스케일링 작업의 Jacobian을 log likelihood에 통합할 필요 없이 이산 데이터의 무손실 codelength임을 보장합니다.

샘플링이 끝나면, 우리는 $\mu_{\theta}(X_{1},1)$을 잡음 없이 표시합니다.

 

위에서 정의된 역방향 과정과 디코더로 방정식 (12)와 (13)에서 파생된 용어로 구성된 변분 경계는 $\theta$에 대해 명확히 미분 가능하고 학습에 사용될 준비가 되어 있습니다.

그러나 우리는 변분 경계의 다음 변형에 대해 훈련하는 것이 샘플 품질에 유익하다 (그리고 구현하기에 간단하다) 는 것을 발견했습니다.

$L_{simple}(\theta)$는 $\epsilon$과 $\epsilon_{\theta}$의 식에서 $t,x_{0},\epsilon$에 대한 기대값으로 정의됩니다.

 

여기서 $t$는 1과 $T$ 사이에서 균일합니다. $t=1$인 경우는 $\sigma^2_{1}$과 edge 효과를 무시하고 빈 폭을 곱한 Gaussian 확률 밀도 함수에 의해 근사된 이산 디코더 정의 (13)의 적분과 함께 $L_{0}$에 해당됩니다.

$t>1$인 경우는 NCSN denoising score matching model에서 사용된 손실 가중치와 유사한 방정식 (12)의 가중되지 않은 버젼에 해당됩니다. (순방향 과정 분산 $\beta_{t}$가 고정되어 있기 때문에 $L_{T}$는 나타나지 않습니다.)

알고리즘 1은 단순화된 목표로 전체 학습 절차를 표시합니다.

 

(14)의 단순화된 목표는 방정식 (12)의 가중치를 버리기 때문에, 이것은 표준 변분 경계와 비교하여 재구성의 다른 측면을 강조하는 가중된 변분 경계입니다.

특히, Section 4의 diffusion 과정 설정은 작은 $t$에 대응하는 가중치 감소 손실 항에 대한 단순화된 목표를 유발하였습니다.

이 항은 매우 작은 양의 잡음과 함께 데이터의 잡음을 제거하도록 네트워크를 학습시키기 때문에 더 큰 $t$ 항의 더 어려운 잡음 제거 과제에 네트워크가 집중할 수 있도록 그것의 가중치를 감소시키는 것이 유익합니다.

우리는 실험에서 이 재가중이 더 나은 샘플 품질로 이어지는 것을 확인할 것입니다.

 

우리는 샘플링 과정에서 필요한 신경망 평가의 수가 이전 작업과 일치하도록 모든 실험에 대해 $T$를 1000으로 설정하였습니다.

우리는 순방향 과정 분산을 $\beta_{1}=10^{-4}$에서 $\beta_{T}=0.02$로 선형적으로 증가하는 상수로 설정하였습니다.

이러한 상수는 [-1, 1]로 스케일링된 데이터에 비해 작게 선택되어 $X_{T}$의 신호-잡음 비율을 최대한 작게 유지하면서 역방향 및 순방향 과정이 거의 같은 함수식을 갖게 합니다.

(우리 실험에서는 $L_{T} = D_{KL}(q(X_{T}|X_{0}) || \mathcal{N}((0,I)) \approx 10^{-5}$의 차원 당 비트 수)

$X_{0}$를 조건으로 하는 $X_{T}$의 분포 $q$와 평균 $0$, 분산 $I$를 갖는 정규 분포 $\mathcal{N}$의 KL divergence 값이 $10^{-5}$에 근사합니다.

 

역방향 프로세스를 나타내기 위해 우리는 그룹 정규화를 통해 마스크되지 않은 PixelCNN++와 유사한 U-Net backbone을 사용하였습니다.

매개변수는 시간을 넘어 공유되며, 이는 Transformer 사인곡선 위치 임베딩을 사용하는 네트워크에 특정됩니다. 우리는 16 X 16 특징 맵 해상도에서 self-attention을 사용했습니다.

 

테이블 1은 CIFAR10에 대한 Inception scores, FID scores, negative log likelihoods (무손실 codelength)를 보여줍니다.

FID score는 3.17으로, 우리의 무조건 모델은 클래스 조건적인 모델들을 포함한 문헌의 대부분의 모델들 보다 좋은 샘플 품질을 달성하였습니다.

우리의 FID score는 표준 관례와 같이 학습 세트에 대해 계산되었습니다. 우리가 시험 세트에 대해 계산했을 때, score는 5.24였고 이것은 문헌의 많은 학습 세트의 FID score보다 여전히 좋은 것이었습니다.

 

예상대로, 실제 변분 경계에서 모델을 학습하는 것이 단순화된 목표에서 학습하는 것보다 더 나은 codelength가 생성되지만 후자가 최상의 샘플 품질을 생성합니다.

 

테이블 2에서, 우리는 역방향 과정 매개변수화와 학습 목표의 샘플 품질 효과를 보였습니다.

우리는 $\tilde{\mu}$를 예측하는 기준 옵션이 방정식 (14)와 유사한 단순화된 학습 목표인, 가중되지 않은 평균 제곱 오차 대신 실제 변분 경계에 대해서 학습했을 때만 잘 작동한다는는 것을 발견했습니다.

우리는 또한 (매개변수화된 대각선 (행렬) $\sum_{\theta}(X_{t})$를 변분 경계에 통합함으로써) 역방향 과정 분산을 학습하는 것이 고정된 분산에 비해서 불안정한 학습과 열악한 샘플 품질로 이어진다는 것을 보았습니다.

$\epsilon$을 예측하는 것은, 우리가 제안한대로, $\tilde{\mu}$를 예측하는 것만큼의 근사적인 성능을 고정된 분산에서 변분 경계에 대해 학습할 때 보이지만, 우리의 단순화된 목표와 함께 학습되었을 때 훨씬 더 좋았습니다.

 

테이블 1은 또한 CIFAR10 모델들의 codelength를 보여줍니다.

학습과 시험 사이의 차이는 차원 당 최대 0.03 비트이며, 이는 다른 likelihood-based 모델에서 보고된 간격과 비슷한 것이며 diffusion model이 과적화되지 않았음을 나타냅니다.

하지만, 우리의 무손실 codelength가 에너지 기반 모델과 annealed 중요도 샘플링을 사용한 score matching 보다 더 낫다고 하더라도, 그들은 다른 유형의 likelihood-based 생성 모델에 비해서는 경쟁력이 없습니다.

 

우리의 샘플들은 그럼에도 불구하고 고품질이기 때문에, 우리는 diffusion model에 그것을 탁월한 손실 압축기로 만드는 귀납적인 편향이 있을 것이라고 결론을 내렸습니다.

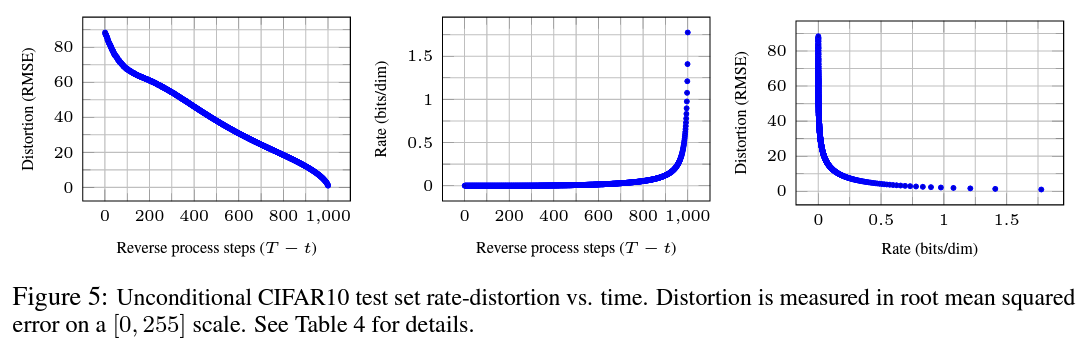
변분 경계 항 $L_{1} + \cdots + L_{T}$을 부호율로 그리고 $L_{0}$를 변형으로 처리하여, 최고 품질의 샘플을 가지는 CIFAR10 모델은 1.78 비트/차원 부호율을 가지고 1.97 비트/차원 변형을 가집니다. 이는 0에서 255까지의 scale에서 0.95의 평균 제곱근 오차에 해당합니다.

무손실 codelength의 절반 이상이 눈에 띄지 않는 변형을 설명합니다.

Inductive Bias란 무엇일까?

 

우리는 방정식 (5)의 형식을 반영하는 점진적 손실 코드를 도입하여 모델의 부호율-변형 동작을 더 자세히 조사할 수 있습니다.

$p$만이 사전에 수신기에서 사용될 수 있는 모든 $p$와 $q$분포에 대해 근사 $D_{KL}(q(X)||p(X))$ 비트를 평균적으로 사용하여 $q(X)$를 따르는 샘플 $X$를 전송할 수 있는 최소 무작위 coding과 같은 절차에 대한 접근을 가정한 알고리즘 3과 4를 보세요.

$X_{0} \sim q(X_{0})$에 적용될 때, 알고리즘 3과 4는 방정식 (5)와 같은 총 기대 codelength를 사용하여 $X_{T}, \cdots , X_{0}$을 순차적으로 전송합니다.

수신기는 어느 $t$ 시점에 대해서도, 완전히 사용할 수 있는 $X_{t}$의 부분 정보를 가지고 있으며 다음을 점진적으로 추정할 수 있습니다.

$X_{t}$로부터 $\hat{X_{0}}$를 계산, 그에 근사한 $X_{0}$를 추정.

 

방정식 (4)에 따라 ($X_{0} \sim p_{\theta}(X_{0}|X_{t})$ 확률적 재구성은 역시 유효하지만, 우리는 그것이 변형을 평가하기 더 어렵게 만들기 때문에 여기에서는 고려하지 않습니다.) 그림 5는 CIFAR10 시험 세트에 대한 결과적 부호율-변형 그래프를 보여줍니다.

각 시간 $t$에서, 변형은 평균 제곱근 오차 $\sqrt{||X_{0} - \hat{X}_{0}||^2/D}$로 계산되고, 부호율은 시간 $t$까지 수신된 누적 비트 수로 계산됩니다.

변형은 부효율-변형 그래프의 낮은-부효율 영역에서 가파르게 감소하여 대부분의 비트가 감지할 수 없는 변형에 실제로 할당되었음을 나타냅니다.

 

우리는  또한 임의의 비트로부터 점진적인 압축해제에 의해 주어지는 점진적인 무조건 생성 과정을 실행하였습니다.

즉, 우리는 알고리즘 2를 이용하여 역방향 과정으로부터 샘플링을 하면서 역방향 과정의 결과, $\hat{X}_{0}$를 예측하였습니다.

그림 6과 10은 역방향 과정의 흐름에서 $\hat{X}_{0}$의 결과적인 샘플 품질을 보여줍니다.

대규모 이미지 특징이 먼저 나타나고 세부 정보가 마지막에 나타납니다.

그림 7은 다양한 $t$에 대해 $X_{t}$가 고정된 확률적 예측 $X_{0} \sim p_{\theta}(X_{0}|X_{t})$를 보여줍니다.

$t$가 작을 때, 세세한 디테일을 제외한 모든 것이 보존되고, $t$가 클 때는, 대규모 특징들만이 보존됩니다.

아마도 이것들이 개념적 압축의 힌트들일 것입니다.

 

변분 경계 방정식 (5)는 다음과 같이 다시 쓸 수 있습니다.

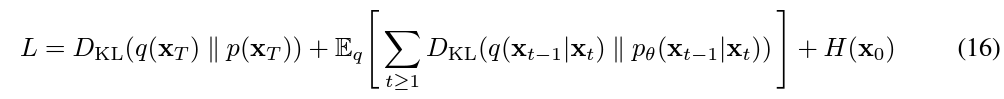
$X_{t}$에 관한 KL divergence의 q에 대한 기대값을 중심으로 표현, 기존의 $L_{T}, L_{t-1}, L_{0}$에서 $L_{T}, L_{0}$를 q에 대한 기대값 밖으로 빼냄.

이제 diffusion 과정 길이 $T$를 데이터의 차원으로 설정하고, 순방향 과정을 정의해 $q(X_{t}|X_{0})$가 모든 확률 질량을 첫 번째 $t$ 좌표를 마스킹하면서 $X_{0}$에 배치시키고(즉, $q(X_{t}|X_{t-1})$가 $t$ 번째 좌표를 가립니다), 빈 이미지에 모든 질량을 배치시키도록  $p(X_{T})$를 설정하고, 그리고 argument를 위해, $p_{\theta}(X_{t-1}|X_{t})$를 완전히 표현적인 조건부 분포로 간주하는 것을 고려해봅니다.

이러한 선택으로 $D_{KL}(q(X_{T})||p(X_{T})) = 0$이 되고,  $D_{KL}(q(X_{t-1}|X_{t})||p_{\theta}(X_{t-1}|X_{t}))$를 최소화하는 것이 $p_{\theta}$를 학습시켜 변경되지 않은 $t+1,\ldots,T$를 복사하고 주어진 $t+1,\ldots,T$로 $t$ 번째 좌표를 예측하도록 합니다.

따라서 이 특정 diffusion으로 $p_{\theta}$를 학습시키는 것은 자동회귀 모델을 학습시키는 것이 됩니다.

 

따라서 우리는 Gaussian diffusion model을 데이터 좌표 재정렬으로 표현될 수 없는 일반화된 비트 순서를 가진 일종의 자동회귀 모델로 해석할 수 있습니다.

이전 작업에서 이러한 재정렬이 샘플 품질에 영향을 주는 귀납적 편향을 도입하는 것을 보였습니다.

때문에 우리는 Gaussian diffusion이 유사한 목적을 수행할 것이며, Gaussian 잡읍이 잡음을 가리는 것보다 이미지에 추가했을 때 더 자연스러 울 수 있기 때문에 아마도 더 큰 영향이 있을 것이라고 추측하였습니다.

또한, Gaussian diffusion 길이는 데이터 차원과 동일하도록 제한되지 않습니다. 예를 들어, 우리는 우리 실험의 32X32X3 또는 256X256X3 이미지 차원보다 더 작은 $T=1000$을 사용합니다.

Gaussian diffusion은 빠른 샘플링을 위해 더 짧게 또는 모델 표현력을 위해 더 길게 만들어 질 수 있습니다.

 

우리는 $q$를 확률적 인코더, $X_{t}, X'_{t} \sim q(X_{t}|X_{0})$로 사용하여 잠재 공간에서 원천 이미지 $X_{0}, X'_{0} \sim q(X_{0})$를 보간할 수있습니다. 그리고 선형 보간된 잠재 $\bar{X}_{t} = (1 - \lambda)X_{0} + \lambda X'_{0}$를 역방향 과정, $\bar{X}_{0} \sim p(X_{0}|\bar{X}_{t})$의 이미지 공간으로 디코딩합니다.

사실상, 우리는 그림 8 (왼쪽)에 묘사된 것처럼 원천 이미지의 손상된 버전을 선형적으로 보간하여 인공물을 제거하는 데 역방향 과정을 사용합니다.

그림 8 (오른쪽)은 원본 CelebA-HQ 256X256 이미지 ($t=500$)의 보간 및 재구성을 보여줍니다.

역방향 과정은 고품질의 재구성과 안경을 제외한 포즈, 피부 톤, 헤어스타일, 표정 및 배경과 같은 속성을 부드럽게 변경시키는 그럴듯한 보간을 생성합니다.

$t$가 클수록 더 거칠고 더 다양한 더 보간이 생성됩니다. 새로운 샘플은 $t=1000$에서 주어집니다.

 

diffusion model은 $q$가 매개변수가 없고 최상위 잠재 $X_{T}$와 데이터 $X_{0}$의 상호 정보가 거의 0이 되도록 설계되었습니다.

우리의 $\epsilon$-예측 역방향 과정 매개변수화는 diffusion model과 샘플링에 annealed Langevin dynamics를 사용한 여러 잡음 레벨에 걸친 잡음 제거 score matching 사이의 연결을 설정하였습니다.

그러나, diffusion model은 간단한 log likelihood 평가를 허용하며, 학습 절차는 변분 추론을 사용하여 Langevin dynamic 샘플러를 명시적으로 학습시킵니다.

연결은 또한 잡음 제거 score matching의 특정 가중 형태가 Langevin-like 샘플러를 훈련시키는 변분 추론과 동일하다는 역방향의 의미를 갖습니다.

우리의 부호율-변형 곡선은 변분 경계의 한 평가에서 시간에 따라 계산되며, annealed 중요도 샘플링의 한 실행에서 변형 페널티에 따라 부호율-변형 곡선을 계산할 수 있는 방법을 연상시킵니다.

우리의 점진적 디코딩 argument는 convolutional DRAW 및 관련 모델에서 볼 수 있으며, 하위 스케일 순서 또는 자동회귀 모델을 위한 샘플링 전략에 대한 보다 일반적인 설계로 이어질 수도 있습니다.

 

우리는 diffusion model을 사용해 고품질 이미지 샘플을 제시하였으며, Markov chain 학습과 잡음 제거 score matching 그리고 annealed Langevin dynamics (그리고 더 나아가 에너지 기반 모델), 자동 회귀 모델과 점진적 손실 압축에 대한 diffusion model과 변분 추론 사이의 연결을 발견하였습니다.

diffusion model이 이미지 데ㅔ이터에 대한 탁월한 귀납적 편향을 가지고 있는 것으로 보이기 때문에, 우리는 다른 데이터 modality와 다른 유형의 생성 모델 및 기계 학습 시스템의 구성요소로서의 유용성을 조사하기를 기대하고 있습니다.

 

안타깝게도 생성 모델을 악의적으로 사용하는 잘 알려진 수많은 사례가 있습니다. (중략)

생성 모델은 훈련된 데이터 세트의 편향을 반영하기도 합니다. 많은 대규모 데이터 세트가 자동화된 시스템에 의해 인터넷에서 수집되기 때문에 특히 이미지에 label이 지정되지 않은 경우 이러한 편향을 제거하기 어려울 수 있습니다.

이러한 데이터 세트에서 훈련된 생성 모델의 샘플이 인터넷 전체에 확산되면 이러한 편향은 더욱 강화될 것입니다.

반면 확산 모델은 데이터 압축에 유용할 수 있습니다. 데이터 압축은 데이터의 해상도가 높아지고 전 세계 인터넷 트래픽이 증가함에 따라 광범위한 청중에게 인터넷 접근성을 보장하는 데 중요할 수 있습니다.

 

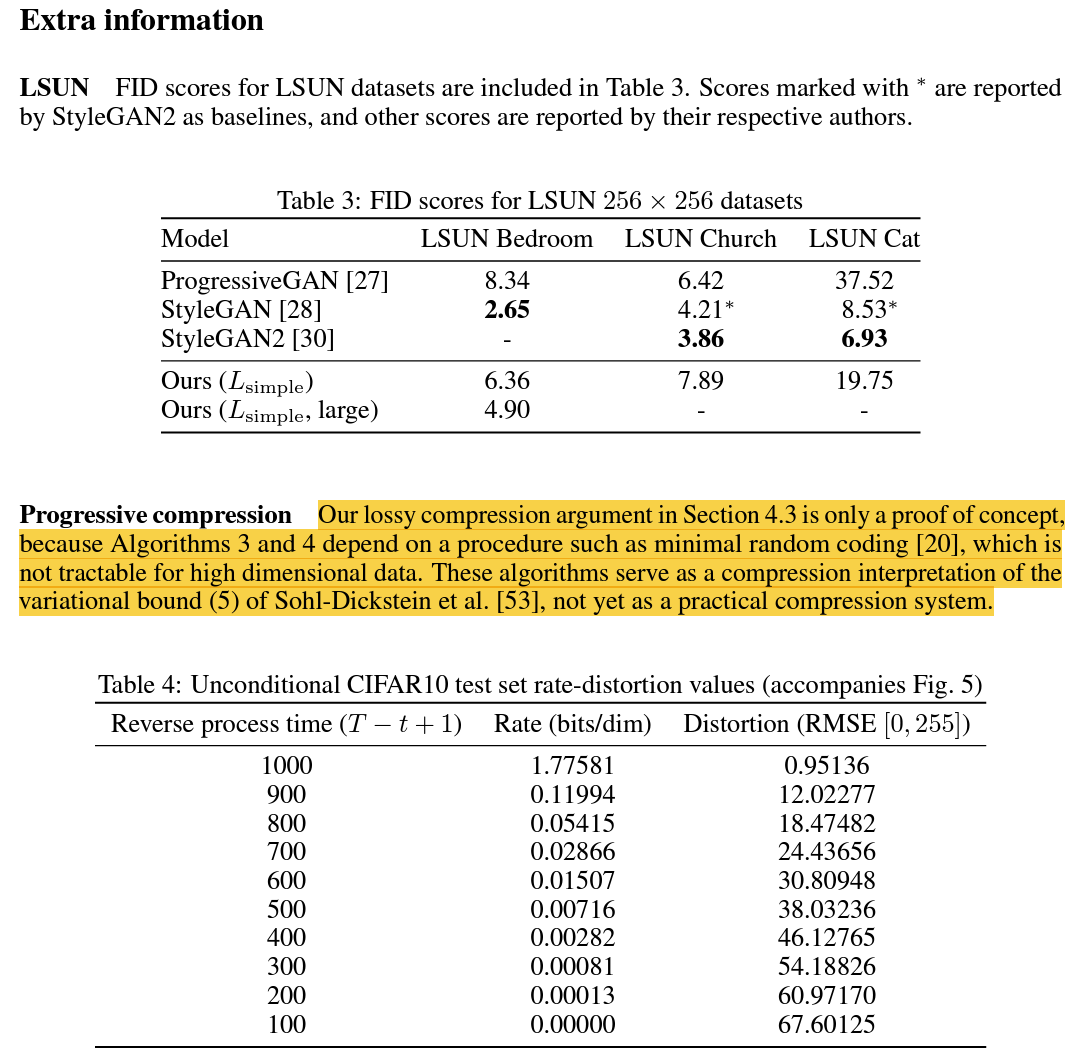
섹션 4.3의 손실 압축 argument는 개념 증명일 뿐입니다. 알고리즘 3과 4가 고차원 데이터에 대해 추적할 수 없는 최소 무작위 코딩과 같은 절차에 의존하기 때문입니다.

이러한 알고리즘들은 Sohl-Dickstein의 변분 경계 방정식 (5)의 압축 해석을 제공하지만 아직 실용적인 압축 시스템은 아닙니다.

 

수식 전개는 따로 해석하지 않겠습니다. 위의 수식 설명 링크를 참고하시기 바랍니다.

 

모델 설정은 밑줄로 대체하겠습니다.

 

하이퍼 파라미터 부분 또한 밑줄로 대체합니다.

 

NCSN과 비교 내용입니다. 따로 번역하지 않고 마무리하겠습니다.

 

샘플링 과정에서, 사전 $X_{T} \sim \mathcal{N}(0,I)$와 Langevin dynamics는 모두 확률적입니다.

잡음의 두 번째 원천의 중요성을 이해하기 위해, CelebA 256X256 데이터 세트에 대해 동일한 중간 잠재성을 조건으로 하는 여러 이미지들을 샘플링했습니다.

그림 7은 $t \in {1000, 750, 500, 250}$에 대한 잠재 $X_{t}$를 공유하는 역방향 과정 $X_{0} \sim p_{\theta}(X_{0}|X_{t})$에서의 여러 추출물들을 보여줍니다.

이를 달성하기 위해서, 우리는 사전의 초기 추출에서 단일 역방향 chain을 실행하였습니다.

중간 단계에서, chain은 분할되어 여러 이미지를 샘플링합니다.

$X_{T=1000}$에서의 사전 추출 후, chain이 분할되면, 샘플들은 크게 달라집니다.

그러나 더 많은 단계 후에 chain이 분할되면, 샘플들은 성별, 머리 색깔, 안경, 채도, 포즈와 표정 같은 높은 수준의 속성을 공유합니다.

이는 $X_{750}$과 같은 중간 잠재들이 그것의 인지 불가성에도 불구하고 이러한 속성들을 인코딩함을 암시합니다.

 

그림 9는 잠재 공간 보간 이전의 diffusion 단계의 수를 변경함에 따른 CelebA 256X256 원천 이미지 쌍 사이의 보간을 보여줍니다. diffusion 단계의 수를 늘리면 원천 이미지에서 더 많은 구조가 파괴되며, 모델은 역방향 과정 중에 이를 완료합니다.

이를 통해 미세한 입도와 거친 입도 모두에서 보간을 할 수 있습니다. 0 단계의 diffusion step으로 제한된 경우, 보간은 원천 이미지를 픽셀 공간에서 혼합합니다.

반면에, 1000단계 diffusion step 이후에 원천 정보가 손실되고 보간은 새로운 샘플이 됩니다.