25. 계산 그래프 시각화(1)
Graphviz
Graph Visualization Software
graphviz.org
26. 계산 그래프 시각화(2)
27. 테일러 급수 미분
미적분학에서 테일러 급수(Taylor級數, 영어: Taylor series)는 도함수들의 한 점에서의 값으로 계산된 항의 무한합으로 해석함수를 나타내는 방법이다.
테일러 급수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 사인 함수의 테일러 급수의 수렴. 검은 선은 사인 함수의 그래프이며, 색이 있는 선들은 테일러 급수를 각각 1차(빨강), 3차(주황), 5차(노랑), 7차(초록), 9차(파랑
ko.wikipedia.org
28. 함수 최적화
p.233 최적화란 어떤 함수가 주어졌을 때 그 최솟값(또는 최댓값)을 반환하는 '입력(함수의 인수)'을 찾는 일입니다. 신경망 학습의 목표도 손실 함수의 출력을 최소화하는 매개변수를 찾는 것이니 최적화 문제에 속합니다.
로젠브록 함수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
p234. 로젠브록 함수가 벤치마크로 자주 쓰이는 이유는 골짜기로 향하는 기울기에 비해 골짜기 바닥에서 전역 최솟값으로 가는 기울기가 너무 작아서 최적화하기 어렵기 때문입니다.
경사 하강법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동
ko.wikipedia.org
29. 뉴턴 방법으로 푸는 최적화(수동 계산)
뉴턴 방법 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 함수 f는 파란 선, 각 접선은 빨간 선이다. 접선의 영점을 반복적으로 취해 나갈 때, xn과 실제 영점의 오차가 점차 줄어듦을 확인할 수 있다. 수치해석학에서 뉴
ko.wikipedia.org
30. 고차 미분(준비 편)
31. 고차 미분(이론 편)
32. 고차 미분(구현 편)
33. 뉴턴 방법으로 푸는 최적화(자동 계산)
34. sin 함수 고차 미분
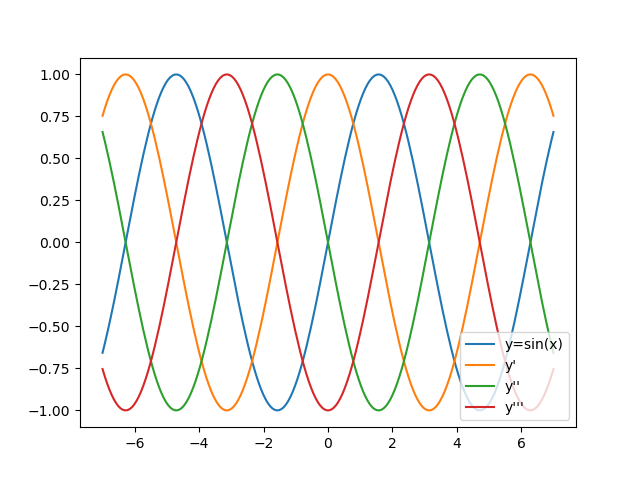
35. 고차 미분 계산 그래프
36. 고차 미분 이외의 용도
'Data > 개념 정리' 카테고리의 다른 글
| [밑러닝 3] 제 5고지, Dezero의 도전 (2) | 2023.02.22 |
|---|---|
| [밑러닝 3] 제 4고지, 신경망 만들기 개념 정리 (2) | 2023.01.28 |
| [밑러닝 3] 제 2고지, 자연스러운 코드로 개념 정리 (1) | 2022.12.10 |
| [밑러닝 3] 제 1고지, 미분 자동 계산 개념 정리 (0) | 2022.11.20 |
| DL/ML Definition & Description (0) | 2022.10.25 |



